Diff算法与实现

Posted on   |   In ,   |   visitors 

什么是Diff

在日常工作中，diff是大家常用的一个工具，它能快速的计算出两个文本的差异，并将差异结果一目了然的展示出来，帮助我们快速定位在不同版本中文件的修改位置。

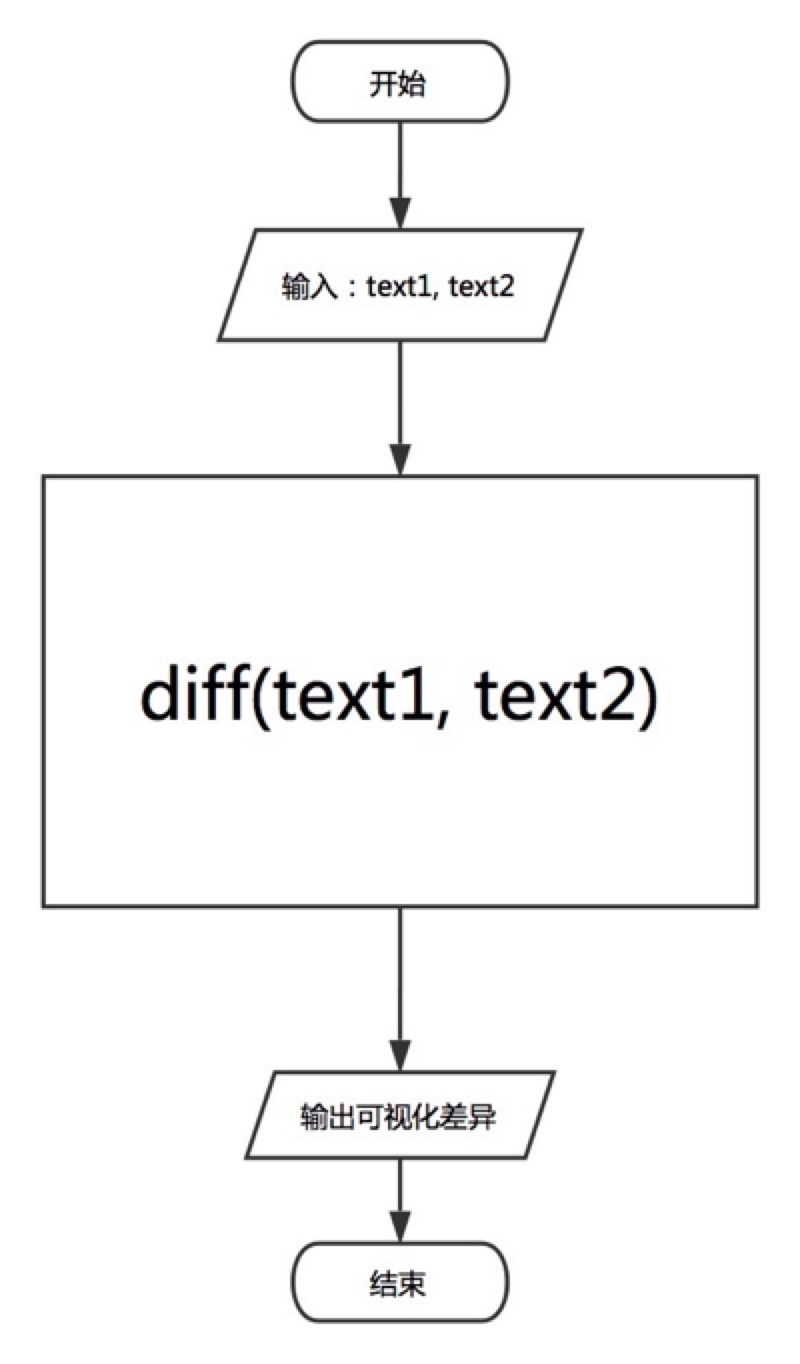
Diff简单流程图

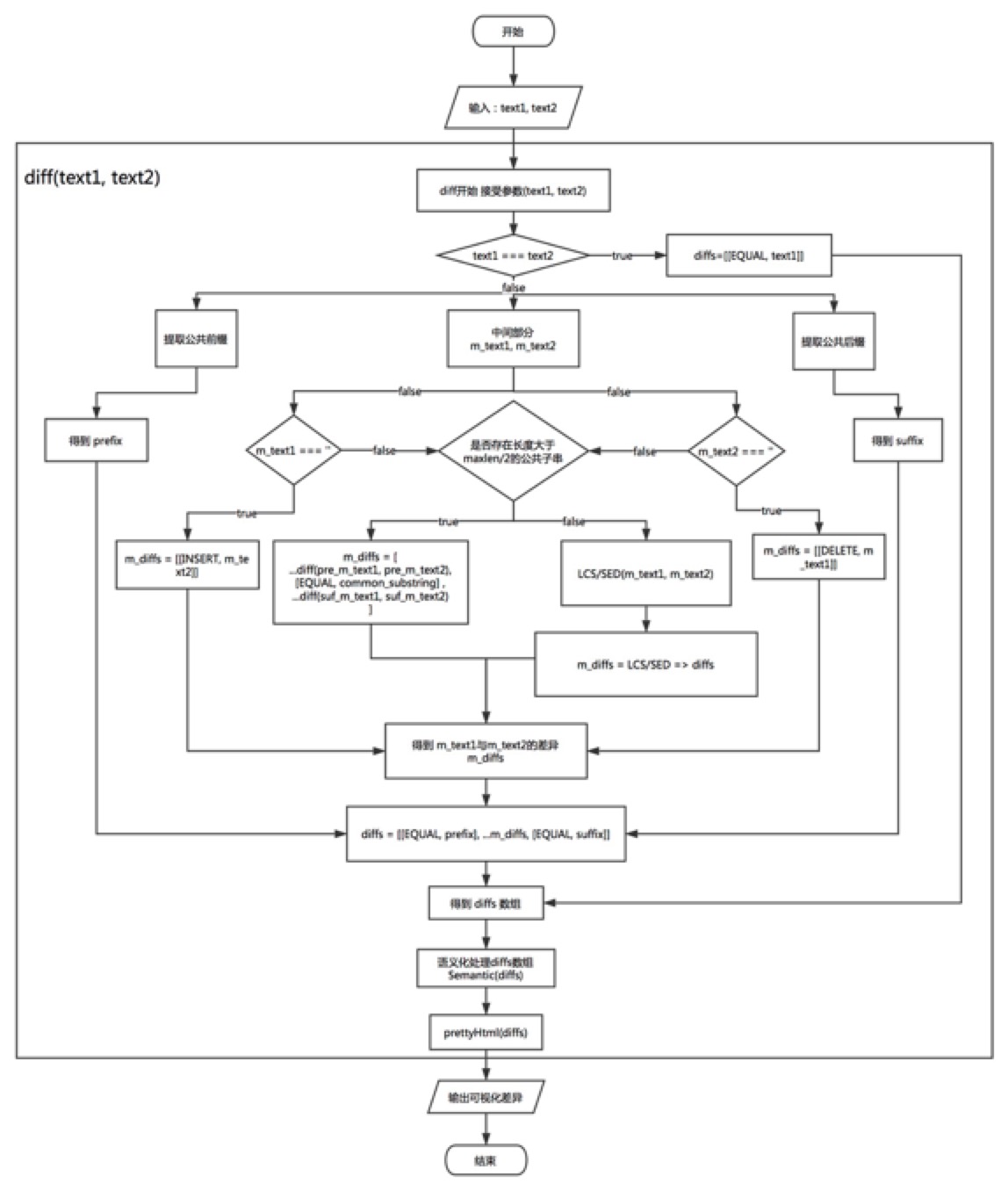
以上流程图简单描述了我们使用diff程序的流程，只需往diff程序中输入text1与text2（我们规定，text1为初始文本，text2为编辑文本），diff程序会自动计算出两个文本的差异并可视化输出。

在这篇文章中，将会简单的谈一谈diff程序内部流程是如何流转并实现的，以及介绍在实现过程中会遇到的一些算法问题。

问题分析

举个简单的例子：

text1: console.log('hello world');
text2: console.log('hi js');

console.log(‘helloi worldjs‘);

从结果中我们可以看出，diff程序的可视化输出，无非是将文本中未改变的部分原样输出，其余字符，若是在text1中，则被标记为删除；若是在text2中，则被标记为新增。如下使用红色标记两个文本的未改变部分：
text1: console.log(‘hello-world‘);
text2: console.log(‘hi-js‘);
红色部分除外，在text1中的ello和world在结果中都将被标记为删除；text2中的i和js在结果中都将被标记为新增。
因此，diff程序的关键就在于如何找到text1与text2所有相同文本（即找到标记红色的文本），然后再分别标记出剩下的删除或新增文本即可。

如何diff

LCS

计算两个文本相同部分的问题，即求两个字符串的最长公共子序列(Longest Common Subsequence，简称LCS)问题，介绍LCS问题解法之前，先了解以下概念。

Subsequence(NOT Substring)

设序列Xm=<x1, x2, …, xm>，从Xm序列中任意取出若干个元素，按照元素下标从小到大的顺序排列得到一个新的序列Zk=<z1, z2, ..., zk>，则Zk为Xm的一个子序列。子序列只要求元素的前后位置关系与原序列中保持一致即可，不必保证元素必需是连续的。

公共子序列

给出两个序列Xm与Yn，找到一个序列Zk，满足：Zk即是Xm的子序列，又是Yn的子序列，则Zk为Xm与Yn的一个公共子序列

最长公共子序列

给出两个序列Xm与Yn，找到一个Xm与Yn的公共子序列Zk，Zk的长度是Xm与Yn所有公共子序列中长度最长的一个。

暴力美学

最简单直接的，就是暴力求解，如下为暴力法求解LCS的伪代码：

Zk = 空
for Xm的所有子序列 Zx
  if Zx是Yn的子序列 && Zx长度大于Zk
    Zk = Zx

一个长度为m的序列，存在2^m个子序列；判断Zx序列是否为Yn序列的子序列，时间复杂度为O(n)；因此暴力求解算法的时间复杂度为O(n*2^m)。指数级别时间复杂度的算法，基本上是要把电脑搞挂的，这显然不是我们想要的结果。

动态规划

动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足，故有时需要引入一定的近似)。简单地说，问题能够分解成子问题来解决。
使用动态规划算法求解最优解的时候，最关键的问题在于如何找到最优解问题的转化方程。

设序列Xm=<x1, x2, …, xm>和Yn=<y1, y2, …, yn>的一个最长公共子序列Zk=<z1, z2, …, zk>，则：

  1. 若xm=yn，可以使用反证法证明：xm(yn)必然是Zk的最后一个字符，即zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列。因此 LCS(X, Y) 即可以转化成 LCS(Xm-1, Yn-1) + 1；
  2. 若xm≠yn且zk≠xm ，亦可用反证法证明：Z是Xm-1和Y的最长公共子序列；
  3. 若xm≠yn且zk≠yn ，同第二点，可得出Z是X和Yn-1的最长公共子序列。
    其中：Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

整合2、3点的结论，得出当xm≠yn时，可以将 LCS(X, Y) 转化成 MAX(LCS(Xm-1, Y), LCS(X, Yn-1))。

设dp[i][j]表示序列Xi和Yj的一个最长公共子序列Zk的长度，即dp[i][j] = k。
因此我们可以得到以下公式：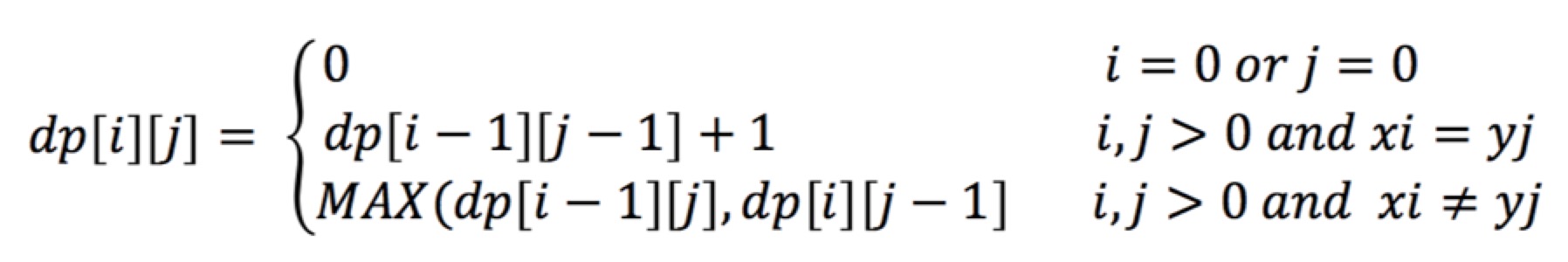
LCS公式

根据此公式，我们定义一个二维数组dp，size为m*n，dp数组中的每个元素的值，都可以通过其左上/左/上三个方位的单元格得到，因此我们只需顺序填满dp表格，在dp[m][n]处就可以得到Xm与Yn的最长公共子序列长度。如下所示(X: ABCABBA, Y: CBABAC)：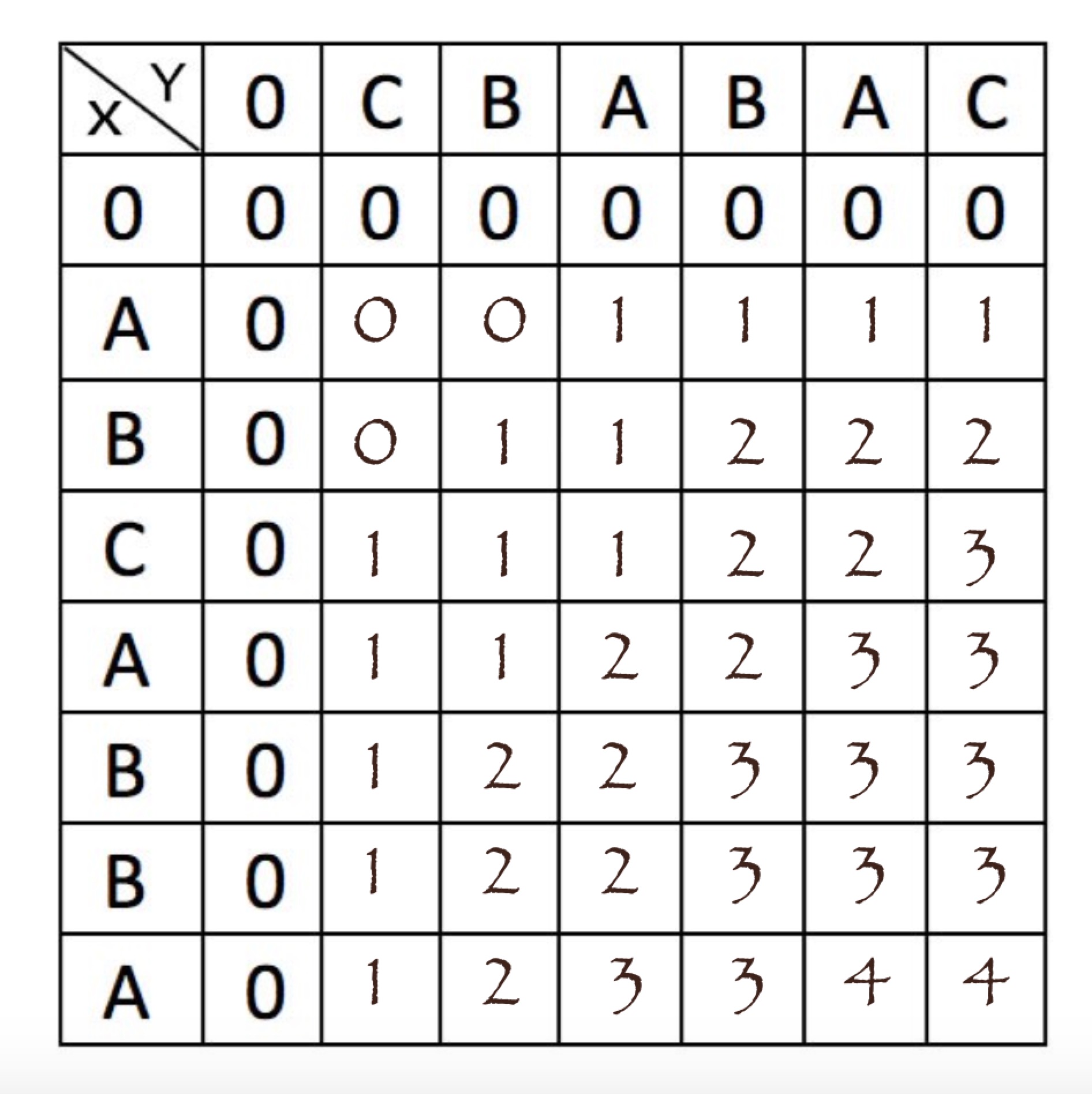
lcs dp表格

仅仅得到最长公共子序列的长度显然不足以达到我们的目的，为了能够得到一个完整的LCS，我们在计算dp表格的过程中，还需要同时记录计算每个单元格值的来源位置，使用↖︎、↑、←三个字符来表示，如下图（若dp[i-1][j]与dp[i][j-1]相等时，默认取左边单元格，即dp[i][j-1]）：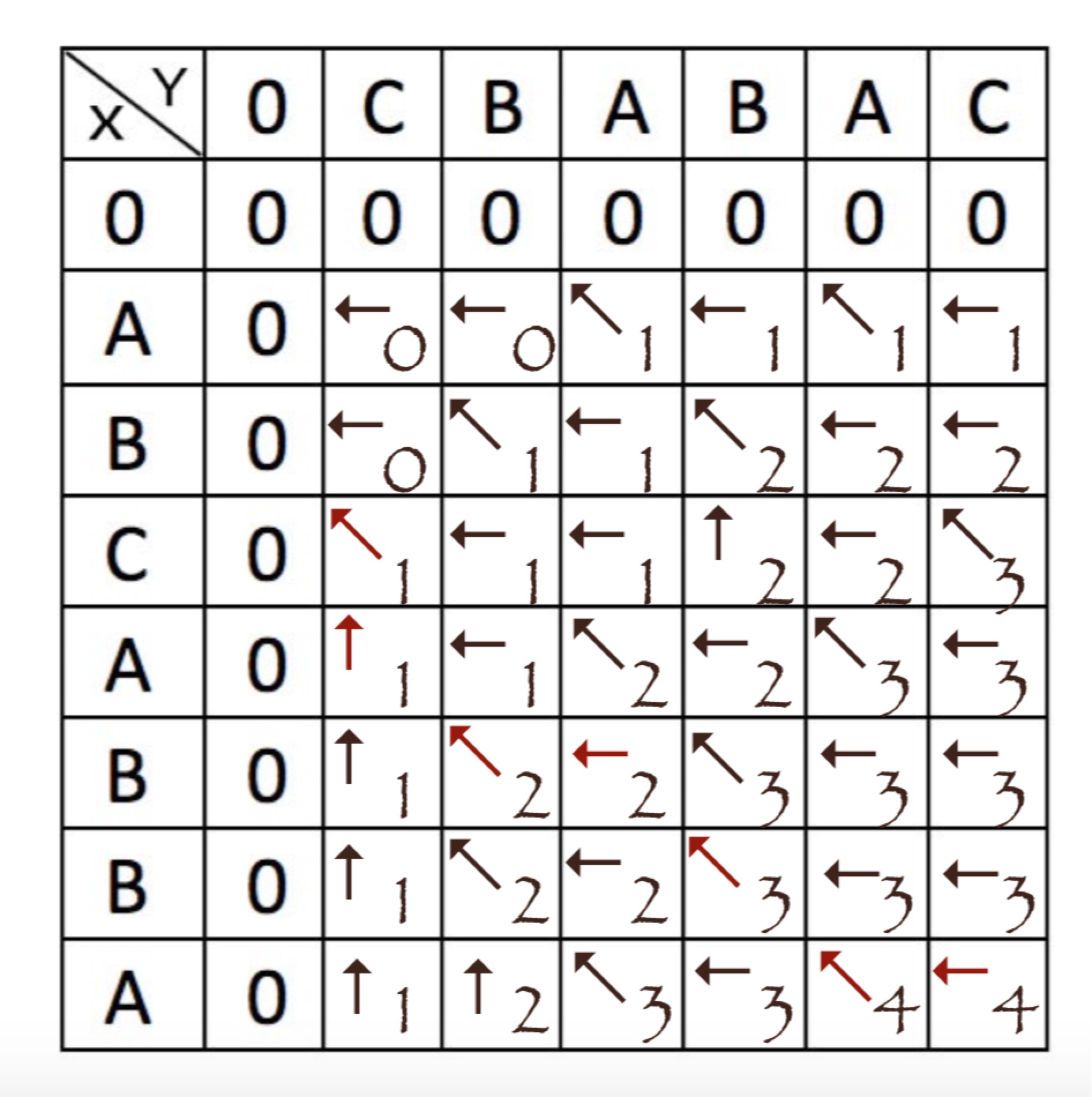
lcs map
在上图的表格中，我们只需要从最右下角的单元格开始，按照箭头的指示就可以一步步往左上角靠近，如图中标记红色的路线。在此路线中，←符号表示Y扫过一个字符，此字符需标记为新增；↑符号表示X扫过一个字符，此字符需标记为删除；↖︎表示X、Y同时扫过一个字符，此字符为LCS中的元素，为未改变字符。
如上操作，我们就可以得到X与Y的一个ABCABABAC

至此我们已经可以实现一个简单的diff程序了。
前往阅读“阉割版”Diff插件源码
点我查看“阉割版”Diff插件Demo演示

SED

除了上面介绍的LCS算法之外，最短编辑距离(Shortest Edit Distance，简称SED)算法同样可以用来实现文本diff。
SED问题的描述是：给出两个字符串text1与text2，求将text1编辑成text2所需要的最短编辑距离。定义有效的编辑操作有：删除一个字符、新增一个字符、替换一个字符，其中一次删除或新增操作编辑距离记为1，替换操作的编辑距离记为2（因为一个替换操作相当于一个删除操作加上一个新增操作）。

仔细观察可以发现，SED问题其实是LCS问题的一个逆向描述。LCS求尽可能多的相同部分，而SED求尽可能少的编辑部分（即不同部分）。他们必然满足一个关系：m + n === 2 * LCS(X, Y) + SED(X, Y); 其中m、n分别为X与Y的长度。因此SED问题的结果与LCS是等效的，求解SED问题同样可以使用动态规划的思想来解，只是在公式上有所不同罢了，以下给出SED的求解公式：

设f[i][j]表示从字符xi转化成yj的编辑距离；
设dp[i][j]表示序列Xi=<x1, x2, …, xi>转化成Yj=<y1, y2, …, yj>的最短编辑距离；

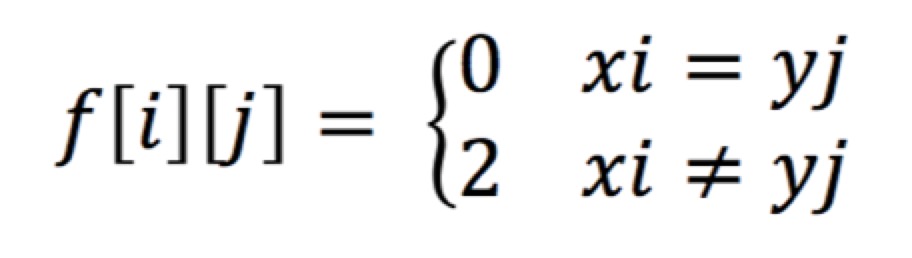
LCS公式 f
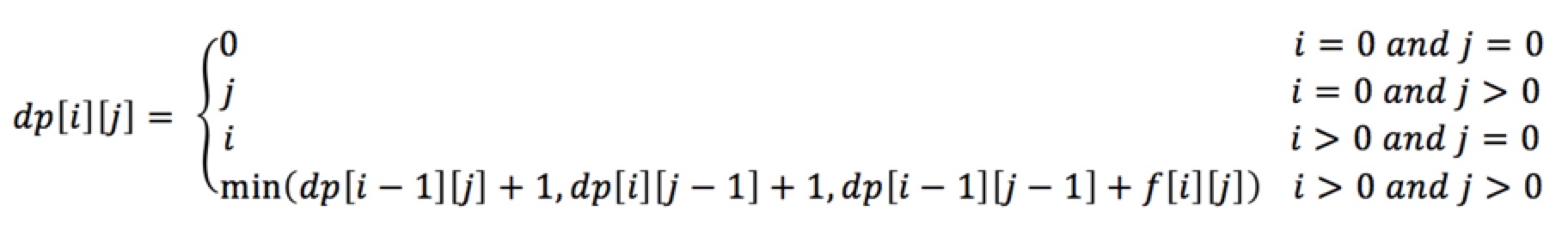
LCS公式 dp

同样，根据公式，依次填满dp表格，同时标记上每个单元格的来源方位，即可找到两个文本的差异，演算过程类似LCS，在此不再赘述。

优化

上面介绍的LCS与SED算法，时间复杂度都是O(n*m)，因此精确计算LCS/SED是非常耗费性能的。
对于基于字符的diff程序，n与m分别为text1与text2的字符数。一个简单有效的优化方式就是转化成基于行的diff，转化后n与m分别为text1与text2的行数，这就可以大大加速diff的耗时，同时也使得diff结果更具语义(svn/git 的diff命令，就是基于行的diff)。

预处理

除了转化成基于行的diff之外，在进行LCS/SED之前，可以进行以下预处理操作来加速diff程序

Equality

简单的判断text1与text2是否全等，可以免去许多不必要的计算。在一个庞大的项目库中，往往每次修改的文件只是其中很小的一部分，因此绝大部分的文件都可以通过判断内容是否全等直接得到结果，无需再进行LCS/SED计算。

Common Prefix/Suffix

提取text1与text2的公共前缀与后缀，再对剩余部分进行diff，可以缩小text1与text2的diff范围。提取公共前缀/后缀的操作，可以使用二分查找的算法，可以在O(logn)的时间复杂度内完成(log以2为底数)。

Singular Insertion/Deletion

在上一步提取完公共前缀/后缀之后，若是text1剩下的为空字符串，则表示仅仅是新增了text2剩下部分的字符串；若是text2剩下的为空字符串，则表示仅仅是删除了text1剩下部分的字符串。因此在这种情况下，也可以直接得到结果，无需再进行LCS/SED计算。

Two Edits

同样再提取公共前缀/后缀之后，剩余部分在头尾都不会有相同的字符，但是在中间部分可能仍有大量的相同部分，若我们能找到剩余部分的一个公共子串，该公共子串可以将text1、text2剩余部分都分割成两个部分[text1_pre, text1_suf]、[text2_pre, text2_suf]，那么我们就可以转化成求diff(text1_pre, text2_pre)和diff(text1_suf, text2_suf)，再将得到的结果拼接在一起，就可以得到完整的diff结果。为了保证这个分割是有效的，可以规定这个公共字串的长度必需大于较长串长度的二分之一。

计算最长公共子串仍然是一个复杂的程序，但是我们可以利用满足长度大于二分之一较长串长度的特殊条件，进行特殊查找即可。

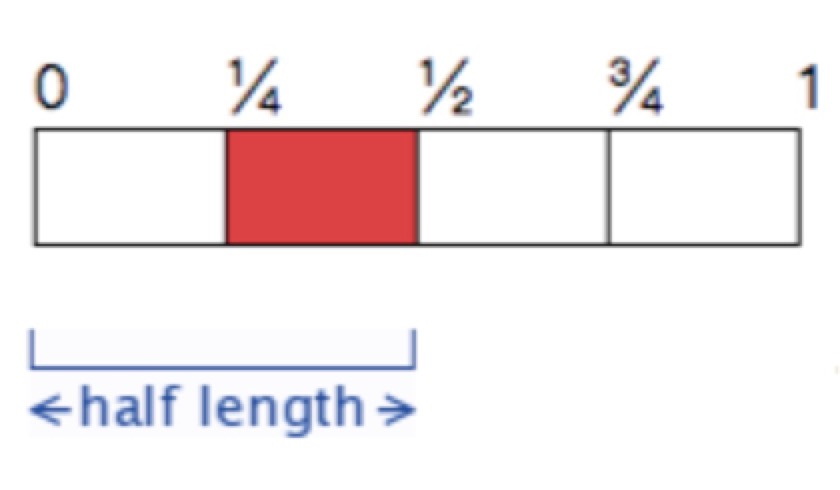
two_edits1

拖动一个二分之一长度的字符串，我们可以发现，这个字符串必然会包含第二个四分之一子串（图中红色部分）或者第三个四分之一子串。利用这个关系，我们只需要分别取这个四分之一子串，判断是否是另一个字符串的子串，若是，则先用此四分之一子串将两个字符串分隔开，如下图所示，分别求前部分的公共后缀，以及后半部分的公共前缀，然后将公共后缀+四分之一子串+公共前缀即可得到一个公共子串，如此求完所有的公共子串，取最长的一个，判断其长度是否大于长串的二分之一即可。

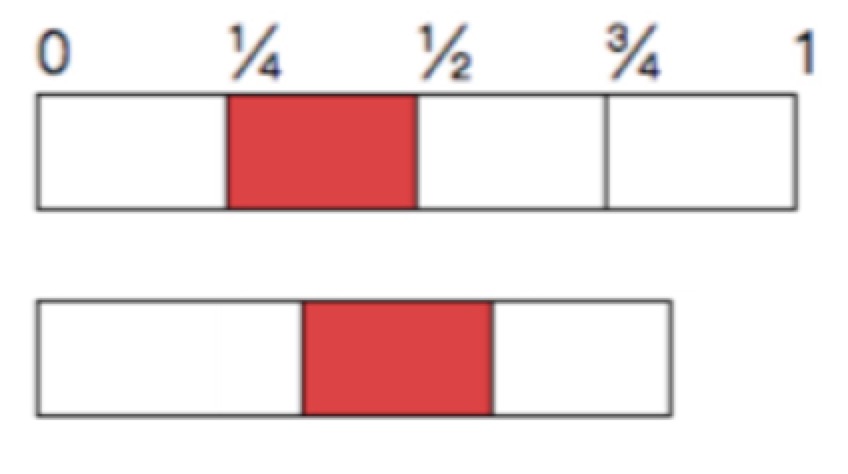
two_edits2

后处理

后处理主要是将前面计算得到的diffs数组进行merge合并，并且做一些语义化的处理，是的输出结果更具语义，利于阅读。

Semantics

对于下图所示的例子，以下计算出的6个diff结果都是等效的。之所以有这么多等效的结果，是因为diffs的编辑具有可移动性。若一个编辑操作的左右两边都是相同部分，满足：

  1. 编辑部分的第一个字符等于其后相同部分的第一个字符，则此编辑部分可右移一个元素；
  2. 编辑部分的最后一个字符等于其前面相同部分的第一个字符，则此编辑部分可左移一个元素。

semantics

这6个diff结果中，显然Diff 3与Diff 4是更具有语义的，因此，我们可以指定一个规则，给每个diff结果进行一个评分，得分高的diff结果，则表示它更具有语义。可以有一下几点评分项目：

  1. 编辑的边界是一个非字母数字字符，1分；
  2. 编辑的边界是一个空白符，2分；
  3. 编辑的边界是一个换行符，3分；
  4. 编辑的边界是一个空行，4分；
  5. 编辑的边界不再是相等部分（移动消耗了整个相等部分），5分。

依据以上几点评分规则，我们可以得到，Diff 1、2、5、6的结果，的0分；Diff 3、4的结果，因为边界分别有两个空白符，因此得4分。所以程序就可以判断出，Diff 3、4得结果，才是更具有语义的。

总结

总结以上的描述，我们可以得出以下完整的Diff程序流程图：

diff程序流程图

阅读资料

Diff Strategies
An O(ND) Difference Algorithm and Its Variations∗

Show comments from Gitment